Tarjan有关连通性相关的基本算法与应用
无向图连通性
Tarjan算法在无向图中的主要用途是求割点、桥、点双连通分量以及边双连通分量。
Tarjan求割点与桥
割点与桥
给定无向连通图 $G = (V, E)$
割点: 对于 $x \in V$ , 从图中删去节点 $x$ 以及所有与 $x$ 连接的边后, 图 $G$ 分裂为两个或两个以上不连通的子图,则称 $x$ 为 $G$ 的割点。
桥/割边: 对于 $e \in V$ , 从图中删去边 $e$ 后, 图 $G$ 分裂为两个或两个以上不连通的子图,则称 $e$ 为 $G$ 的桥/割边。
时间戳
在DFS中,按照每个节点第一次被访问的时间顺序,依次给予 $N$ 个节点 $1 \sim N$ 的标记,该标记就被称为时间戳,记为 $dfn[x]$ ,需要注意 $dfn[x]$ 不是唯一的, $dfn[x]$ 的值与它的搜索顺序有关。
搜索树
对一个无向连通图进行DFS时,把所有发生递归的边 $(x, y)$ (即 $x$ 到 $y$ 是对 $y$ 的第一次访问) 构成一棵树,这棵树就是搜索树。
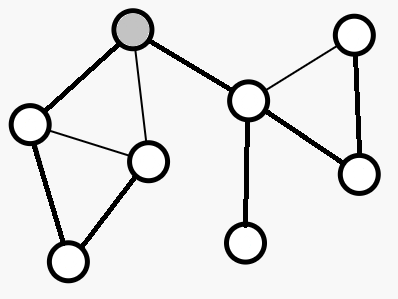
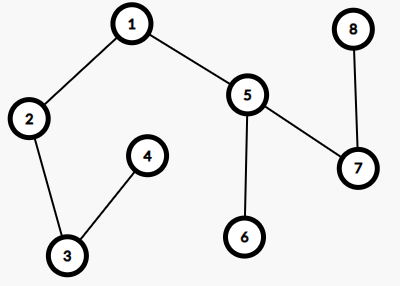
上方两图中上图是一张无向连通图,灰色的点是DFS的起点,加粗的边是发生递归的边;下图是标注了时间戳后的搜索树。
追溯值
追溯值 $low[x]$ 是Tarjan算法的关键,追溯值 $low[x]$ 表示DFS中,点 $x$ 通过除了到自己父节点的边以外的边(即通过1条不在搜索树上的边)可回溯到的最早时间点。
根据定义,为了计算 $low[x]$ 需要先令 $low[x] = dfn[x]$ ,然后进行递归。
递归时,若搜索树上的 $x$ 是 $y$ 的父节点,则用 $low[y]$ 来更新,即 $low[x] = min(low[x], low[y])$ ;若无向边 $(x, y)$ 不是搜索树上的边,则用 $dfn[y]$ 进行更新,即 $low[x] = min(low[x], dfn[y])$
下面是求无向图中追溯值 $low[x]$ 的参考代码
void tarjan(int x)
{
dfn[x] = low[x] = ++timer; //生成时间戳, 并令low[x] = dfn[x]
for(int i = head[x]; i; i = edge[x].next) //链式前向星遍历
{
int y = edge[i].to;
if(!dfn[y]) //在搜索树上x是y的父节点
{
tarjan(y);
low[x] = min(low[x], low[y]);
}
else //无向边(x, y)不是搜索树上的边
low[x] = min(low[x], dfn[y]);
}
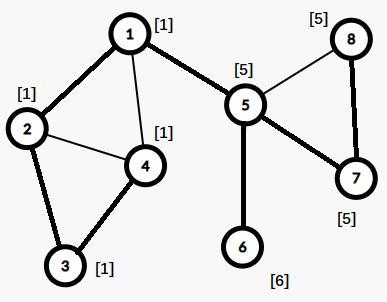
}下图是上图中各个点的 $low[x]$ 值
求割边
对于无向边 $(x, y)$ ,当且仅当搜索树上存在 $x$ 的一个子节点 $y$ 满足:$dfn[x]<low[y]$ 时,边 $(x,y)$ 是割边。
$dfn[x]<low[y]$ 说明从以 $y$ 为根的子树出发,在不经过无向边 $(x, y)$ 的情况下,无论怎么走,都无法到达 $x$ 或比 $x$ 更早的节点,即无向边 $(x, y)$ 是割边。
由此也可以发现两个规律:
- 割边一定是搜索树中的边
- 一个简单环中的边一定都不是割边
在代码实现的时候需要注意,由于我们遍历的是无向图,所有从每个点 $x$ 出发,都能访问到它的父节点 $fa$ ,但根据 $low[x]$ 的定义,无向边 $(x, fa)$ 一定是搜索树上的边,且 $fa$ 不是 $x$ 的子节点,所以不能使用 $dfn[fa]$ 来更新 $low[x]$。
但是,如果我们在DFS时只记录 $x$ 的父节点 $fa$ 无法解决重边的情况,因为 $x$ 和 $fa$ 之间存在重边时,边 $(x, fa)$ 一定不是割边,在这些重边中,只有一条是“搜索树上的边”,故有重边时,可以使用 $dfn[fa]$ 来更新 $low[x]$
对于上述情况有一个更好的解决方案,将记录 $fa$ 改为记录“递归进入每个节点的边的编号”。因为处理的是无向图,所以每条无向边可以看成两条成对的有向边,这两条有向边是成对存储的,如果建边时边的编号从2开始,那么成对储存的编号就是“2和3”,“4和5”,“6和7”···。而异或可以实现 $2\ xor\ 1 = 3$ ,$3\ xor\ 1 = 2$ , $4\ xor\ 1 = 5$ , $5\ xor\ 1 = 4$ ··· ,所以沿着编号为 $i$ 的边递归进入了节点 $x$ 时,可以忽略从 $x$ 出发的编号为 $i \ xor \ 1$ 的边,通过其他边求追溯值 $low[x]$ 。
下面是求割边的参考代码
struct Edge
{
int to, next;
}edge[M];
int head[N], dfn[N], low[N];
bool bridge[N]; //bridge[i] - 边i是否是桥
int timer, tot;
void addedge(int u, int v)
{
edge[++tot].next = head[u];
edge[tot].to = v;
head[u] = tot;
}
void tarjan(int x, int in_edge)
{
dfn[x] = low[x] = ++timer;
for(int i = head[x]; i; i = edge[x].next)
{
int y = edge[i].to;
if(!dfn[y])
{
tarjan(y, i);
low[x] = min(low[x], low[y]);
if(low[y] > low[x]) //判断割边
bridge[i] = bridge[i ^ 1] = 1; //无向边对应的两条有向边都打上桥的标记
}
else if(i != (in_edge ^ 1))
low[x] = min(low[x], dfn[y]);
}
}
int main()
{
int n, m;
cin >> n >> m;
tot = 1; //tot从2开始记录,用于异或
for(int i = 1; i <= n; i++)
{
int x, y;
cin >> x >> y;
addedge(x, y);
addedge(y, x);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) //处理存在多个连通块的情况
tarjan(i, 0); //tarjan求桥
for(int i = 2; i < tot; i += 2)
if(bridge[i])
cout << edge[i ^ 1].to << ' ' << edge[i].to << '\n';
return 0;
}求割点
割点的判定条件有两种情况:
- 若 $x$ 不是搜索树的根节点,则存在 $x$ 的一个子节点 $y$ 满足: $dfn[x] \leq low[y]$ 时, $x$ 是割点。
- 若 $x$ 是搜索树的根节点,则 $x$ 当且仅当存在两个子节点 $y_1, y_2$ 满足: $dfn[x] \leq low[y]$ 时, $x$ 是割点。
上面两条判定条件的证明和割边判定条件的证明类似,$dfn[x \leq low[y]$ 说明从以 $y$ 为根节点的子树出发,如果不经过 $x$ ,无论怎么走都无法到达比 $x$ 更早的点,即 $x$ 是割点。
下面是求割点的参考代码
struct Edge
{
int next, to;
}edge[M];
int head[N], dfn[N], low[N];
bool iscut[N]; //iscut[i] - 点i是否是割点
int timer, root, cnt, tot; //root - 当前搜索树的根节点, cnt - 图中的割点数目
void addedge(int u, int v)
{
edge[++tot].next = head[u];
edge[tot].to = v;
head[u] = tot;
}
void tarjan(int x)
{
dfn[x] = low[x] = ++timer;
int son = 0; //当前点连接的满足dfn[x] <= low[y]的子节点的数目
for(int i = head[x]; i; i = edge[i].next)
{
int y = edge[i].to;
if(!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if(low[y] >= dfn[x]) //割点判断条件
{
son++; //满足条件的子节点加一
if(x != root || son > 1) //判断x是搜索树的根节点时是否满足条件
{
cnt += !iscut[x];
iscut[x] = 1;
}
}
}
else
low[x] = min(low[x], dfn[y]);
}
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int x, y;
cin >> x >> y;
addedge(x, y);
addedge(y, x);
}
for (int i = 1; i <= n; i++)
if (!dfn[i])
root = i, tarjan(i); //记录当前搜索树的根节点,求割点
cout << cnt << '\n';
for(int i = 1; i <= n; i++)
if(iscut[i])
cout << i << ' ';
return 0;
}Tarjan求双连通分量
点双连通分量与边双连通分量
点双连通分量:若一张无向连通图不存在割点,则称它为点双连通图,无向图的极大点双连通子图被称为点双连通分量,简记为v-DCC。
边双连通分量:若一张无向连通图不存在桥,则称它为边双连通图,无向图的极大边双连通子图被称为边双连通分量,简记为e-DCC。
以上二者统称为双连通分量,简记为DCC。
相关定理
一张无向连通图是点双连通图,当且仅当满足下列两个条件之一:
- 图的顶点数不超过2
- 图中任意两点都同时包含在至少一个简单环中(简单环:除了第一个顶点和最后一个顶点相同外,其余顶点不重复出现的回路叫简单环)
一张无向连通图是边双连通图,当且仅当满足下一条件:
图中任意一条边都包含在一个简单环中
求边双连通分量
边双连通分量的求法是求出无向图中所有的桥,将桥全部删去后,无向图会分成若干个连通块,每个连通块就是一个边双连通分量。
还是上面的图,将图中的桥(1, 5),(5, 6)删去后,剩下的连通块就是边双连通分量了

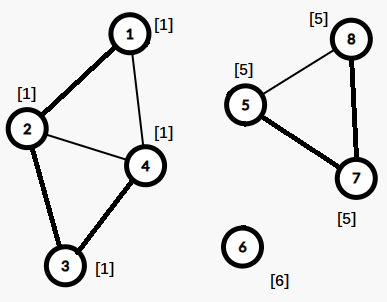
在代码实现上,可以先用Tarjan算法求出所有的桥,再对整个无向图进行一次DFS,划分出每个连通块。
下面是求边双连通分量的参考代码
struct Edge
{
int to, next;
}edge[M];
int head[N], dfn[N], low[N], dcc[N]; //dcc[i] - 点i所属的边双连通分量的编号
bool bridge[N];
int timer, tot, dcctot; //dcctot - 边双连通分类数量
void dfs(int x) //dfs划分连通块
{
dcc[x] = dcctot;
for(int i = head[x]; i; i = edge[i].next)
{
int y = edge[i].to;
if(dcc[y] || bridge[i])
continue;
dfs(y);
}
}
int main()
{
int n, m;
cin >> n >> m;
tot = 1;
for(int i = 1; i <= n; i++)
{
int x, y;
cin >> x >> y;
addedge(x, y);
addedge(y, x);
}
for(int i = 1; i <= n; i++)
if(!dfn[i])
tarjan(i, 0);
//以上为求割边的操作, tarjan函数的代码和上面求割边的一样
for(int i = 1; i <= n; i++)
{
if(!dcc[i]) //当前点还未被访问
{
dcctot++; //边双连通分量数加一
dfs(i);
}
}
return 0;
}边双连通分量的缩点
将每个e-DCC视为一个节点,把割边视为节点间的无向边,可以将原来的图缩为一棵树或多棵树,这样可以便于处理一些问题。
下面给出缩点的参考代码
struct Edge
{
int to, next;
}edge_c[M]; //缩点得到的新图
int head_c[N];
int tot_c;
void addedge_c(int u, int v) //新图的加边函数
{
edge_c[++tot_c].next = head_c[u];
edge_c[tot_c].to = v;
head_c[u] = tot_c;
}
int comb() //缩点函数
{
for(int i = 2; i <= tot; i++)
{
int x = edge[i ^ 1].to, y = edge[i].to;
if(dcc[x] != dcc[y])
addedge_c(dcc[x], dcc[y]);
}
}
int main()
{
int n, m;
cin >> n >> m;
tot = 1;
for(int i = 1; i <= n; i++)
{
int x, y;
cin >> x >> y;
addedge(x, y);
addedge(y, x);
}
for(int i = 1; i <= n; i++)
if(!dfn[i])
tarjan(i, 0);
for(int i = 1; i <= n; i++)
{
if(!dcc[i])
{
dcctot++;
dfs(i);
}
}
//以上为求边双连通分量的操作
comb(); //缩点函数
return 0;
}求点双连通分量
若某点为孤立点,则它自己可以单独构成一个v-DCC,除孤立点外,v-DCC的大小至少为2。与桥和e-DCC的关系不同,桥不属于任何e-DCC,但是割点可能属于多个v-DCC,比如下面的例子,不同颜色圈起来的是不同的v-DCC。
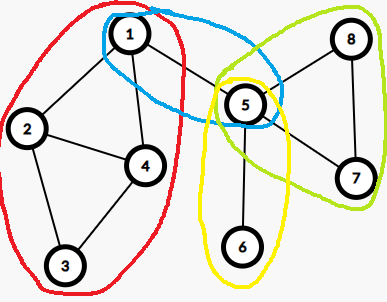
由图可知,图中有4个v-DCC,且存在一个割点属于多个v-DCC的情况。
求点双连通分量需要创建一个栈,并在Tarjan算法的过程中维护该栈,维护方法如下:
- 当节点第一次被访问时,将节点入栈
- 当 $dfn[x] \leq low[y]$ 成立时,无论 $x$ 是否为根,都需要从栈中不断弹出节点,直到 $y$ 出栈,并将所有弹出的节点与 $x$ 一起构成一个v-DCC
上述操作的参考代码如下
struct Edge
{
int to, next;
}edge[M];
int head[N], dfn[N], low[N];
bool iscut[N];
int timer, tot, dcctot, root; //dcctot - 点双连通分量的数量
vector<int> dcc[N]; //dcc[i] - 点双连通分量i中的点的编号
stack<int> st; //用于求v-DCC的栈
void tarjan(int x)
{
dfn[x] = low[x] = ++timer;
st.push(x);
int son = 0;
if(x == root && head[x] == 0) //特判孤立点
{
dcc[++dcctot].push_back(x);
return;
}
for(int i = head[x]; i; i = edge[x].next)
{
int y = edge[i].to;
if(!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if(low[y] >= dfn[x])
{
son++;
if(x != root || son > 1)
iscut[x] = 1;
int top; //栈顶元素
dcctot++; //v-DCC数量加一
do
{
top = st.top();
st.pop();
dcc[dcctot].push_back(top);
} while (top != y); //进行上述第二步操作
dcc[dcctot].push_back(x);
}
else
low[x] = min(low[x], dfn[y]);
}
}
}点双连通分量的缩点
由于一个割点可能在多个v-DCC中,所以缩点相比e-DCC更复杂一些,设图中共有 $p$ 个割点和 $t$ 个v-DCC。我们建立一张包含 $p + t$ 个节点的新图,把v-DCC和割点作为新图的节点,并在这些点之间连边,最后得到的新图是一棵树或多棵树。
下面是v-DCC缩点的参考代码
void comb(int n)
{
int num = dcctot;
for(int i = 1; i <= n; i++) //给每个割点新的编号
if(iscut[i])
new_id[i] = ++num;
tot_c = 1;
for(int i = 1; i <= dcctot; i++) //建新图, 从每个v-DCC到它包含的所有割点连边
{
for(int j = 0; j < dcc[i].size(); i++)
{
int x = dcc[i][j];
if(iscut[x])
{
addedge_c(i, new_id[x]);
addedge_c(new_id[x], i);
}
else
vdcc[x] = i; //除割点外,其他点只属于一个v-DCC
}
}
}有向图连通性
Tarjan算法在有向图中的用途主要是求强连通分量,求出强连通分量后可以将原图缩点成为一个DAG(有向无环图),在DAG上便可进行拓扑排序、DP等操作来解决问题
Tarjan求强连通分量
强连通分量
在一张有向图中,若对于图中任意两个节点 $x$ , $y$ ,即存在从 $x$ 到 $y$ 的路径,也存在从 $y$ 到 $x$ 的路径,则称该有向图是强连通图。有向图的极大强连通子图被称为强连通分量,简记为SCC。其中极大意味着将图分为多个强连通分量后,不存在两个强连通分量间互相可达。
边的分类
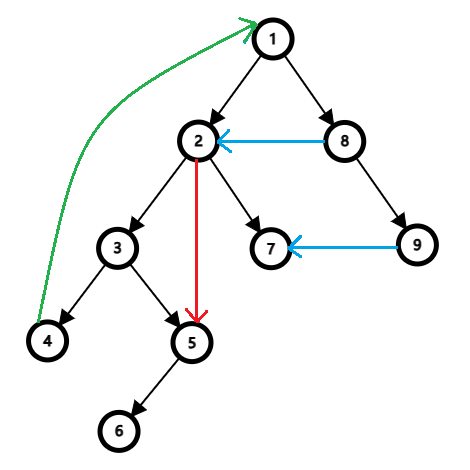
除了生成树的树边外,原图剩下的边可以分为三种:
前向边(红色线):某个点到它子树上的点的边,前向边对强连通分量的构成没有帮助。
反向边(绿色线):某个点到它的某个祖先的边,这种边会产生环,是形成强连通分量的关键。
横插边(蓝色线):某个点到既非祖先也非子树上的点,这种边不会产生强连通分量,但是可能可以扩大强连通分量的范围。
追溯值
$low[x]$ 表示 $x$ 通过有向边,可回溯到的最早的时间戳。
可以通过以下步骤得到追溯值
- 当节点 $x$ 第一次被访问时,令 $low[x] = dfn[x]$ ,将 $x$ 入栈
遍历从 $x$ 出发的每条边 $(x, y)$
(1) 若 $y$ 未被访问过,说明 $(x, y)$ 是树边,递归访问 $y$ ,之后更新 $low[x] = min(low[x], low[y])$
(2) 若 $y$ 被访问过且当前 $y$ 在栈中,则更新 $low[x] = min(low[x], dfn[y])$
- 在 $x$ 相连的边都遍历完后,若 $low[x] = dfn[x]$ ,则 $x$ 为强连通分量的根,将栈中元素不断出栈,直到 $x$ 出栈,到这里所有出栈的元素就是一个强连通分量
求强连通分量
Tarjan算法求强连通分量的过程就和上面表述的一样,算法学习笔记(69): 强连通分量 - 知乎 (zhihu.com)这个笔记里有比较详细的图例和过程讲解。
下面给出求强连通分量的参考代码
struct Edge
{
int to, next;
}edge[M];
int head[N], dfn[N], low[N], scc[N]; //scc[i] - 点i所属的强连通分量的编号
bool inst[N]; //inst[i] - 点i是否在栈中
int tot, timer, scctot; //scctot - 强连通分量的数量
stack<int> st; //储存元素的栈
void tarjan(int cur)
{
dfn[cur] = low[cur] = ++timer;
st.push(cur); //将当前点入栈
inst[cur] = 1;
for(int i = head[cur]; i; i = edge[i].next)
{
int to = edge[i].to;
if(!dfn[to]) //当前to未被访问过
{
tarjan(to); //进入递归
low[cur] = min(low[cur], low[to]);
}
else if(inst[to]) //在栈中则更新low[cur]
low[cur] = min(low[cur], dfn[to]);
}
if(dfn[cur] == low[cur]) //cur为当前强连通分量的根
{
scctot++;
int top;
do
{
top = st.top();
st.pop();
scc[top] = cur;
inst[top] = 0;
if(top != cur)
a[cur] += a[top];
} while (top != cur);
}
}强连通分量的缩点
强连通分量的缩点也比较简单,和边双连通分量缩点比较类似,将强连通分量视为一个节点,将节点连起来即可
下面是参考代码
void comb(int n)
{
for(int i = 1; i <= n; i++)
for(int j = head[i]; j; j = edge[j].next)
if(scc[i] != scc[edge[j].to]) //当前边上的起点与终点不属于同一强连通分量
addedge_c(scc[i], scc[edge[j].to]);
}强连通分量缩点后可以形成一个DAG图,之后可以进行许多应用。
比如 P3387 【模板】缩点,题目给出 $n$ 个点和 $m$ 条边,每个点具有权值,求一条路径使得经过的点权之和最大,可以多次经过同一个点,但重复的点权值只会算一次。
这题可以先将一个每个点带有点权的有向图缩点为每个点带点权的DAG,之后进行拓扑排序和DP即可解决问题,下面是参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = 1e5 + 10;
struct Edge
{
int to, next;
}edge[M], edge_c[M];
int head[N], head_c[N], dfn[N], low[N], scc[N], a[N], dp[N], ind[N];
bool inst[N];
int tot, tot_c, timer, scctot;
stack<int> st;
void addedge(int u, int v)
{
edge[++tot].next = head[u];
edge[tot].to = v;
head[u] = tot;
}
void addedge_c(int u, int v)
{
edge_c[++tot_c].next = head_c[u];
edge_c[tot_c].to = v;
head_c[u] = tot_c;
}
void tarjan(int cur)
{
dfn[cur] = low[cur] = ++timer;
st.push(cur);
inst[cur] = 1;
for(int i = head[cur]; i; i = edge[i].next)
{
int to = edge[i].to;
if(!dfn[to])
{
tarjan(to);
low[cur] = min(low[cur], low[to]);
}
else if(inst[to])
low[cur] = min(low[cur], dfn[to]);
}
if(dfn[cur] == low[cur])
{
scctot++;
int top;
do
{
top = st.top();
st.pop();
scc[top] = cur;
inst[top] = 0;
if(top != cur)
a[cur] += a[top];
} while (top != cur);
}
}
void comb(int n)
{
for(int i = 1; i <= n; i++)
for(int j = head[i]; j; j = edge[j].next)
if(scc[i] != scc[edge[j].to])
{
addedge_c(scc[i], scc[edge[j].to]);
ind[scc[edge[j].to]]++;
}
}
int get_ans(int n)
{
queue<int> q;
for(int i = 1; i <= n; i++)
{
if(scc[i] == i && !ind[i])
{
q.push(i);
dp[i] = a[i];
}
}
while(!q.empty())
{
int x = q.front();
q.pop();
for(int i = head_c[x]; i; i = edge_c[i].next)
{
int y = edge_c[i].to;
dp[y] = max(dp[y], dp[x] + a[y]);
ind[y]--;
if(ind[y] == 0)
q.push(y);
}
}
int ret = 0;
for(int i = 1; i <= n; i++)
ret = max(ret, dp[i]);
return ret;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> a[i];
for(int i = 1; i <= m; i++)
{
int u, v;
cin >> u >> v;
addedge(u, v);
}
for(int i = 1; i <= n; i++)
if(!dfn[i])
tarjan(i);
comb(n);
cout << get_ans(n) << '\n';
return 0;
}题目列表
| 序号 | 题号 | 标题 | 题型 | 难度评级 |
|---|---|---|---|---|
| 1 | luogu - P3388 | 【模板】割点(割顶) | 割点 | ⭐ |
| 2 | POJ - 1523 | SPF | 割点 | ⭐⭐ |
| 3 | luogu - P5058 | 嗅探器 | 割点 | ⭐⭐ |
| 4 | luogu - P3225 | 矿场搭建 | 割点 | ⭐⭐⭐ |
| 5 | POJ - 3352 | Road Construction | 边双连通分量 | ⭐⭐ |
| 6 | HDU - 2460 | Network | 边双连通分量 | ⭐⭐⭐ |
| 7 | HDU - 3394 | Railway | 点双连通分量 | ⭐⭐ |
| 8 | HDU - 3749 | Financial Crisis | 点双连通分量 | ⭐⭐⭐ |
| 9 | HDU - 1269 | 迷宫城堡 | 强连通分量 | ⭐ |
| 10 | luogu - P2863 | The Cow Prom S | 强连通分量,缩点 | ⭐ |
| 11 | luogu - P2341 | 受欢迎的牛 G | 强连通分量,缩点 | ⭐⭐ |
| 12 | luogu - P2746 | 校园网Network of Schools | 强连通分量,缩点 | ⭐⭐ |
| 13 | luogu - P1407 | 稳定婚姻 | 强连通分量 | ⭐⭐ |
| 14 | luogu - P3387 | 【模板】缩点 | 强连通分量,缩点 | ⭐⭐⭐ |
| 15 | luogu - P2515 | 软件安装 | 强连通分量,缩点 | ⭐⭐⭐ |
| 16 | luogu - P2272 | 最大半连通子图 | 强连通分量,缩点 | ⭐⭐⭐ |
参考资料
《算法竞赛进阶指南》 李煜东 大象出版社
Tarjan与无向图的连通性_aWty_的博客-CSDN博客
点双连通分量&边双联通分量详解_Hypoc_的博客-CSDN博客
强连通分量(tarjan算法) · CSGrandeur/s-1problem1day1ac · Discussion #479 (github.com)