搜索与树的基本概念与简单算法
搜索
搜索是一种常见且通用的算法,本节课主要介绍两种比较基础的搜索算法: 深度优先搜索(DFS),广度优先搜索(BFS)
深度优先搜索 (DFS)
DFS算法的主要思想是“一路到底,逐步回退”,实现方法主要是递归,接下来用 洛谷P1605 迷宫 这题作为例题来讲解一下DFS算法。
这题的题目大意是给出一个大小为 $N \times M$ 的网格图,网格图中有 $T$ 处障碍物,现在给出图中的起点 $S$ 与终点 $F$ ,求出从 $S$ 到 $F$ 共有多少种路径。
另外,题目的数据范围 $1 \le N,M \le 5$
对于这样的数据范围较小,答案与路径有关的题目,我们一般会选择DFS。
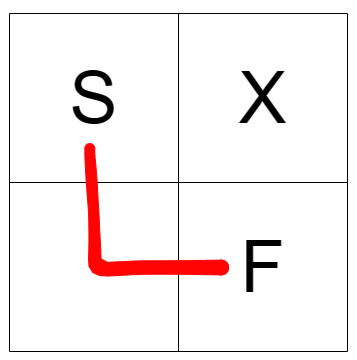
上图是样例中的情况,显然只有一条路径。样例提供的情况太过简单,我们可以自己出一种更为复杂的情况来看看。
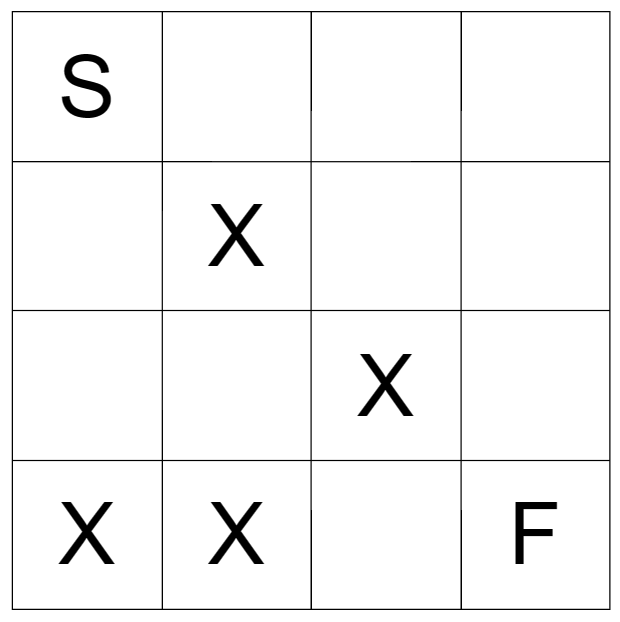
为了在这个网格图上进行遍历,我们可以先规定一个遍历的顺序,比如 [下,上,右,左],意思就是如果能向下走,则向下走一格,否则向上走一格,按规定的顺序以此类推。如果以上的四个方向都走不了或到达了终点,则进行回溯。另外,遍历的时候要记录我们已经走过的地方,已经走过的则不再走,同样回溯的时候我们需要将走过的点变为没走过的点。
实现代码入下:
#include <bits/stdc++.h>
using namespace std;
const int N = 10;
bool vis[N][N]; // 判重数组
int dx[4] = {1, -1, 0, 0}; // 遍历顺序: 下 上 右 左
int dy[4] = {0, 0, 1, -1};
int n, m, sx, sy, fx, fy, ans;
void dfs(int x, int y)
{
if (x == fx && y == fy) // 递归终点: 走到了终点, 返回上一状态
{
ans++;
return;
}
for (int i = 0; i < 4; i++) // 遍历四个方向
{
int xx = x + dx[i], yy = y + dy[i];
if (xx >= 1 && xx <= n && yy >= 1 && yy <= m && !vis[xx][yy]) // 判断要走到的点是否合法, 是否走过
{
vis[xx][yy] = 1; // 下一个要走的点标记为走过
dfs(xx, yy);
vis[xx][yy] = 0; // 回溯
}
}
return;
}
int main()
{
int t;
scanf("%d%d%d%d%d%d%d", &n, &m, &t, &sx, &sy, &fx, &fy);
for (int i = 1; i <= t; i++)
{
int x, y;
scanf("%d%d", &x, &y);
vis[x][y] = 1; // 将障碍物不能走到, 可以视为已经走过的点
}
vis[sx][sy] = 1; // 设置起点为已经走过的状态
dfs(sx, sy);
printf("%d", ans);
return 0;
}从上面的例题中我们可以总结出DFS代码的基本框架:
void dfs()
{
if (...) // 递归终点, 满足条件
{
//对答案更新
return;
}
for (...) // 枚举当前状态下的下一步情况
{
if (!vis[i]) // 判断当前状态是否出现过, 没出现过则进入下一步
{
vis[i] = 1; // 对当前状态标记
dfs(i);
vis[i] = 0; // 回溯
}
}
return;不过DFS的题目比较灵活,以上模板并不泛用,还是需要对思想进行理解。
广度优先搜索 (BFS)
BFS的主要思想是“全面扩散,逐层递进”,实现主要依靠队列,下面以 洛谷P1443 马的遍历 作为例题讲解BFS算法。
题目给出一个网格图与马所在的坐标,要求出马到网格图上每个点最少需要几步。
对于这类需要求出最短距离的题目,我们一般使用BFS。
对于样例中的情况我们可以画图模拟: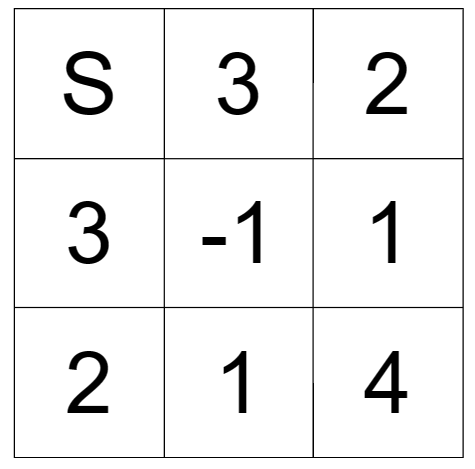
得到上图的具体过程如下:
走一步后我们可以到达(3, 2)或(2, 3),也就是我们从(1, 1)这一点扩展出了两个状态,我们借助队列这一数据结构来顺序存储状态。
所以我们将上面的两个点存入队列,并记录存入队列的点为已经走过的点,接下来不再走。接着对队列中的元素按顺序进行扩展,即可扩展完整张图,这时马走到每个点需要的步数即为马到每个点的最少步数,这是BFS层层递进的特点,因为BFS采用的是一层一层往下走,所以对某一点的第一次访问一定是最近的一次。
实现代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 410;
int dis[N][N]; // 记录最短距离
bool vis[N][N]; // 记录该点是否被走过
int n, m;
int dx[8] = {1, 1, 2, 2, -1, -1, -2, -2}; // 马的移动
int dy[8] = {2, -2, 1, -1, 2, -2, 1, -1};
void bfs(int fx, int fy)
{
queue<pair<int, int>> q; // 用于存储的队列
q.push({fx, fy}); // 将起点存入
vis[fx][fy] = 1; // 标记起点为已访问
dis[fx][fy] = 0; // 起点的步数为0
while (q.size()) // 队列不为空
{
int x = q.front().first, y = q.front().second; // 取队首元素的位置, 也就是我们这一次循环所在的点
q.pop(); // 弹出队首元素
for (int i = 0; i < 8; i++) // 遍历马的八个移动方向
{
int xx = x + dx[i], yy = y + dy[i];
if (xx >= 1 && xx <= n && yy >= 1 && yy <= m && !vis[xx][yy]) // 判断访问的点是否合法, 是否走过
{
dis[xx][yy] = dis[x][y] + 1; // 要走的点的步数为当前点步数加1
vis[xx][yy] = 1; // 标记已访问过
q.push({xx, yy}); // 将要走的点放入队列
}
}
}
}
int main()
{
int x, y;
scanf("%d%d%d%d", &n, &m, &x, &y);
bfs(x, y);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (!vis[i][j])
printf("-1 ");
else
printf("%d ", dis[i][j]);
}
printf("\n");
}
return 0;
}从上面的例题中我们可以总结出BFS代码的基本框架:
void bfs(int fx)
{
queue<...> q; // 依据状态选择队列的数据类型
q.push(fx); // 将起始状态存入
vis[fx] = 1; // 对起始状态初始化
while (!q.empty())
{
int x = q.front().first, y = q.front().second; // 取队首元素
q.pop(); // 弹出队首元素
for (...) // 遍历下一状态
{
if (!vis[xx]) // 判断访问状态是否合法
{
// 通过当前状态递推下一状态
vis[xx] = 1; // 对状态标记
q.push(...); // 将要走的点放入队列
}
}
}
}树
本节课主要讲树的基础,包括定义,存储以及遍历。
树的定义
一个没有固定根结点的树称为 无根树。无根树有几种等价的形式化定义:
- 有 $n$ 个结点,$n - 1$ 条边的连通无向图
- 无向无环的连通图
- 任意两个结点之间有且仅有一条简单路径的无向图
- 任何边均为桥的连通图
- 没有圈,且在任意不同两点间添加一条边之后所得图含唯一的一个圈的图
在无根树的基础上,指定一个结点称为 根,则形成一棵 有根树。有根树在很多时候仍以无向图表示,只是规定了结点之间的上下级关系。
有关树的定义
适用于无根树与有根树
- 森林:每个连通分量(连通块)都是树的图。按照定义,一棵树也是森林。
- 生成树:一个连通无向图的生成子图,同时要求是树。也即在图的边集中选择 $n - 1$ 条,将所有顶点连通。
- 无根树的叶结点:度数不超过 $1$ 的结点。
- 有根树的叶结点:没有子结点的结点。
以上的定义都涉及一些图论的知识,现在仅作了解。
适用于有根树
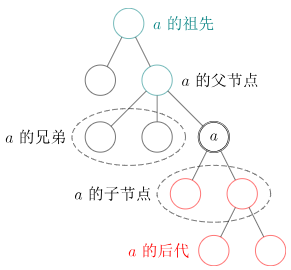
- 父亲:对于除根以外的每个结点,定义为从该结点到根路径上的第二个结点。根结点没有父结点。
- 子结点:如果 $u$ 是 $v$ 的父亲,那么 $v$ 是 $u$ 的子结点。除了二叉树以外,子结点的顺序一般不加以区分。
- 兄弟:同一个父亲的多个子结点互为兄弟。
- 祖先:一个结点到根结点的路径上,除了它本身外的结点。根结点的祖先集合为空。
- 后代:子结点和子结点的后代。或者理解成:如果 $u$ 是 $v$ 的祖先,那么 $v$ 是 $u$ 的后代。
- 结点的深度:到根结点的路径上的边数。
- 树的高度:所有结点的深度的最大值。
- 子树:删掉与父亲相连的边后,该结点所在的子图。
特殊的树
- 二叉树:每个结点最多只有两个儿子(子结点)的有根树称为二叉树。常常对两个子结点的顺序加以区分,分别称之为左子结点和右子结点。
大多数情况下,二叉树 一词均指有根二叉树。 - 完整二叉树:每个结点的子结点数量均为 0 或者 2 的二叉树。换言之,每个结点或者是树叶,或者左右子树均非空。
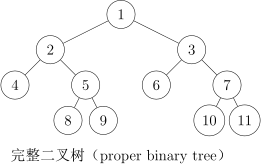
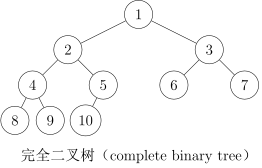
- 完全二叉树:只有最下面两层结点的度数可以小于 2,且最下面一层的结点都集中在该层最左边的连续位置上。
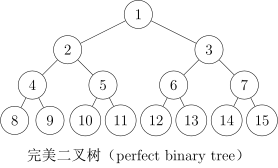
- 完美二叉树:所有叶结点的深度均相同,且所有非叶节点的子节点数量均为 2 的二叉树称为完美二叉树,也叫满二叉树。
树的存储
只记录父节点
可以通过创建一个数组 $pa[N]$ 来记录某一结点的父节点,比如 $v$ 的父节点是 $u$ ,即 $pa[v] = u$ ,这种方式虽然书写简单,但是记录的信息较少,只能自底向上访问。
邻接表
可以通过创建一个vector数组 $e[N]$ 来记录某一结点所连接的其他节点,比如 $u$ 连接了 $v1,v2,v3$ 三个点,则可以用 e[u].push_back(v1), e[u].push_back(v2), e[u].push_back(v3) 来表示。在有根树中,可以用 $e[N]$ 来记录某一点的子节点,再结合上一种方法中的 $pa[N]$ 来实现记录。
这种方法是最常使用的方法。
二叉树的存储
二叉树的存储需要特别记录左右子节点,可以用如下方式表示:
int parent[N]; //父节点
int lch[N], rch[N]; //左子节点和右子节点树的遍历
树上DFS
树上DFS的过程为:先访问根节点,接着分别访问根节点的每个子树
void dfs(int cur)
{
vis[cur] = 1;
for(int son : e[cur]) //for(int i = 0; i < e[cur].size(); i++)
if(!vis[son])
dfs(son);
}树上BFS
树上BFS的过程为:访问根节点,将与根节点相连的点入队,接着不断将队首元素作为根节点来进行更新。
void bfs(int s)
{
queue<int> q;
q.push(s);
vis[s] = 1;
while(q.size())
{
int cur = q.front();
q.pop();
for(int to : e[cur])
{
if(!vis[to])
{
vis[to] = 1;
q.push(to);
}
}
}
}二叉树DFS
与树上DFS不同,二叉树的DFS可以通过遍历的顺序分为先序遍历,中序遍历,后序遍历三种。
先序遍历
按照 根,左,右 的顺序遍历二叉树。
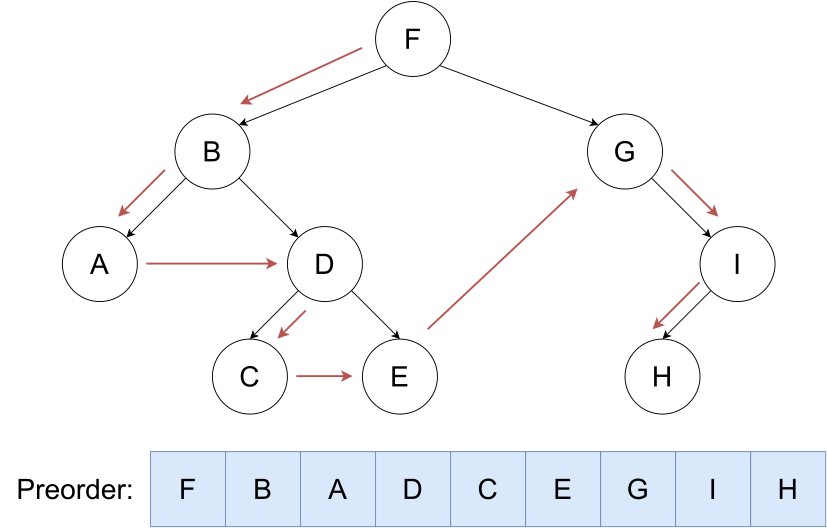
void preorder(int cur)
{
if(cur)
{
printf("%d ", cur);
preorder(lch[cur]);
preorder(rch[cur]);
}
}中序遍历
按照 左,根,右 的顺序遍历二叉树。
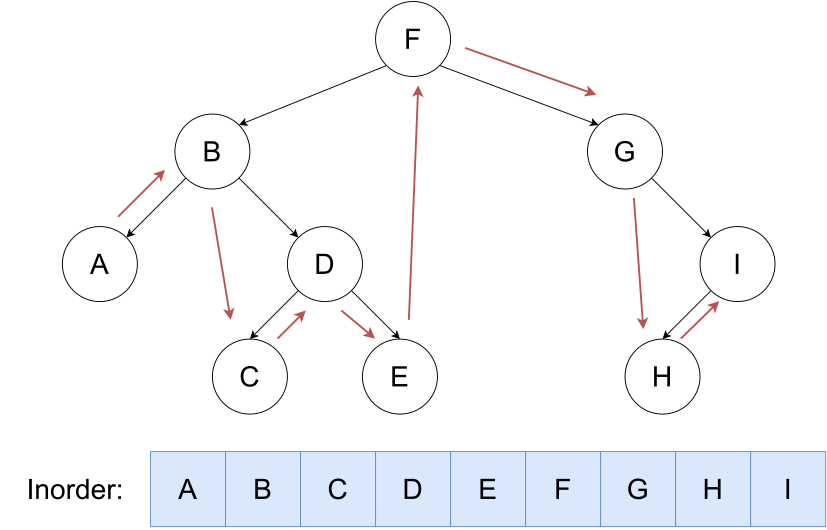
void inorder(int cur)
{
if(cur)
{
inorder(lch[cur]);
printf("%d ", cur);
inorder(rch[cur]);
}
}后序遍历
按照 左,右,根 的顺序遍历二叉树。
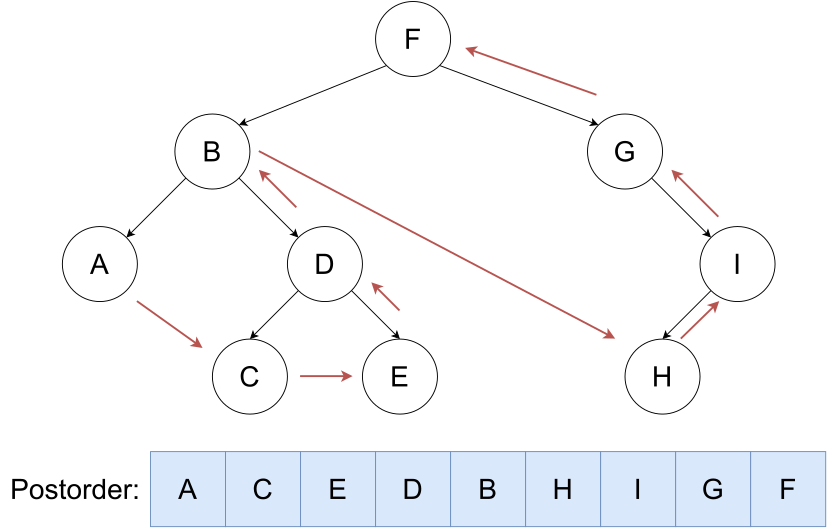
void postorder(int cur)
{
if(cur)
{
postorder(lch[cur]);
postorder(rch[cur]);
printf("%d ", cur);
}
}题单
| 序号 | 题号 | 标题 | 题型 | 难度评级 |
|---|---|---|---|---|
| 1 | 洛谷 - P1605 | 迷宫 | DFS | ⭐ |
| 2 | 洛谷 - P1443 | 马的遍历 | BFS | ⭐ |
| 3 | 洛谷 - P1162 | 填涂颜色 | BFS | ⭐ |
| 4 | OpenJ_Bailian - 1321 | 棋盘问题 | DFS | ⭐⭐ |
| 5 | OpenJ_Bailian - 4123 | 马走日 | DFS | ⭐⭐ |
| 6 | OpenJ_Bailian - 2816 | 红与黑 | DFS/BFS | ⭐⭐ |
| 7 | 洛谷 - P1135 | 奇怪的电梯 | DFS/BFS | ⭐⭐ |
| 8 | OpenJ_Bailian - 4127 | 迷宫问题 | DFS/BFS | ⭐⭐ |
| 9 | 洛谷 - P2895 | Meteor Shower S | BFS | ⭐⭐⭐ |
| 10 | 洛谷 - P1825 | Corn Maze S | BFS | ⭐⭐⭐ |
| 11 | 洛谷 - P1219 | 八皇后 Checker Challenge | DFS | ⭐⭐⭐ |
| 12 | 洛谷 - P1019 | 单词接龙 | DFS | ⭐⭐⭐ |
| 13 | 洛谷 - P5908 | 猫猫和企鹅 | 树上DFS | ⭐ |
| 14 | 洛谷 - P1305 | 新二叉树 | 二叉树 | ⭐ |
| 15 | 洛谷 - P4913 | 二叉树深度 | 二叉树 | ⭐⭐ |