最短路的一些进阶应用
Dijkstra
Dijkstra算法是一种单源最短路算法,一次计算能得到从一个起点到其他所有点的最短距离长度。Dijkstra算法是一种高效且稳定的算法,使用优先队列优化的Dijkstra的时间复杂度是 $O(mlogn)$ ,但是只能在边权全部为正的情况下使用Dijkstra算法,一旦存在负边权就不能使用。
Dijkstra算法的主要思想是BFS+贪心,对于Dijkstra算法的实现寒期集训已经介绍过了,这里就不再赘述,给出参考代码:
struct Node
{
int to, w, next;
}edge[M << 1]; //处理无向图的时候M需要乘2
int head[N], dis[N], vis[N], tot, n, m, s;
priority_queue<pair<int, int> > q;
void add(int x, int y, int z) //链式前向星建图
{
edge[++tot].to = y;
edge[tot].w = z;
edge[tot].next = head[x];
head[x] = tot;
}
void dijkstra(int s)
{
memset(dis, INF, sizeof(dis));
memset(vis, 0, sizeof(vis));
dis[s] = 0;
q.push(make_pair(0, s));
while(!q.empty())
{
int x = q.top().second;
q.pop();
if(vis[x])
continue;
vis[x] = 1;
for(int i = head[x]; i; i = edge[i].next)
{
int y = edge[i].to, z = edge[i].w;
if(dis[y] > dis[x] + z)
{
dis[y] = dis[x] + z;
q.push(make_pair(-dis[y], y));
}
}
}
}Floyd
Floyd算法是一种多源最短路算法,一次计算能得到图中每对节点之间的最短路径。Floyd算法的效率不高,时间复杂度为 $O(n^3)$ ,可以处理负边权,但不能处理负环,所以在某些情况下需要判断负环。
Floyd算法的思路比较类似于动态规划,Floyd算法的实现同样也在寒期集训时介绍过了,这里也是给出参考代码:
int dp[N][N], n, m;
int main()
{
scanf("%d%d", &n, &m);
memset(dp, 0x3f3f3f3f, sizeof(dp));
for(int i = 1; i <= m; i++)
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
dp[u][v] = w;
dp[v][u] = w;
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
printf("%d\n", dp[1][n]);
return 0;
}Bellman-Ford
这一部分是本专题的重要部分,因为接下来的判断负环和差分约束都需要借助这一算法或这一算法衍生出的SPFA算法来解决。
Bellman-Ford算法是单源最短路算法,多用于处理带负边权的图,并且可以对图中是否有负环进行判断。它的时间复杂度为 $O(mn)$ 。
接下来介绍一下Bellman-Ford算法的原理:一个有 $n$ 个点的图,给每个点 $n$ 次机会查询邻居,是否有起点 $s$ 的更短的路径,如果有就更新;经过 $n$ 轮查询和更新,就得到了所有点到起点 $s$ 的最短路径。
Bellman-Ford算法的实现也比较简单,只要对每条边进行 $n - 1$ 次松弛即可,参考代码如下:
void bellman(int s)
{
memset(dis, INF, sizeof(dis));
dis[s] = 0;
for(int i = 1; i <= n - 1; i++) //进行n - 1次
for(int j = 1; j <= tot; j++) //对每条边进行松弛
if(dis[edge[j].v] > dis[edge[j].u] + edge[j].w)
dis[edge[j].v] = dis[edge[j].u] + edge[j].w;
}这里再解释一下为什么要进行 $n - 1$ 次松弛,因为要对所有的边进行松弛,但是我们此时无法保证边的顺序是 $v_1 → v_2, v_2 → v_3, ···, v_{n - 1} → v_n$ 的顺序,所以松弛需要进行多次,由于每一轮的松弛都是对所有边进行松弛,那么第一轮一定包含 $v_1 → v_2$ ,第二轮包含 $v_2 → v_3$ ,第 $n - 1$ 轮包含 $v_{n - 1} → v_n$ ,结合这所有 $n - 1$ 轮的顺序,最后一定可以得出 $v_1 → v_2, v_2 → v_3, ···, v_{n - 1} → v_n$ 的顺序,也就得到了最短路的结果,接下来用下面的图来举一个简单的例子:
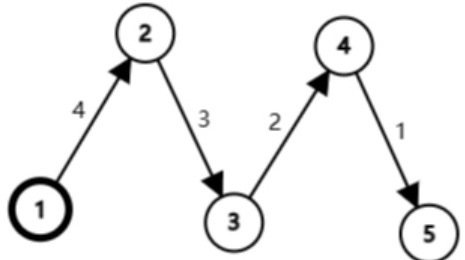
假设图中的所有边边权都为1,图中写在边上的数字代表边的编号,接下来我们模拟一下Bellman-Ford算法来求出 $v_1 → v_5$的最短距离:
第1轮:首先将 $dis[1]$ 设为0,松弛边1,也就是 $v_4 → v_5$ ,更新 $dis[5] = 1$ ,接着松弛边2,更新 $dis[4] = 1$ ,以此类推,第一轮结束后除点1以外所有点的dis值均为1
第2轮:依次松弛边1,边2,边3,更新 $dis[5] = dis[4] = dis[3] = 2$ ,接着松弛边4,此时 $dis[2] = dis[1] + w(1 → 2)$ ,不再更新
···
第4轮:按顺序对各边进行松弛,此时 $dis[1],dis[2],dis[3],dis[4]$ 均不更新,仅更新 $dis[5] = 4$ ,至此我们得到了点1到其余所有点的最短距离
SPFA
SPFA算法是队列优化的Bellman-Ford算法,改进方法是每轮计算只更新上一轮有变化的那些点的邻居,而那些没有变化的点不需要更新它们的邻居。SPFA算法在一般情况下时间复杂度一样,但是在最差的情况下会达到 $O(mn)$ 。
SPFA的实现包括四个执行步骤:
1.起点 $s$ 入队,计算所有邻居到 $s$ 的最短距离,接着 $s$ 出队,状态有更新的邻居入队。
2.当前队列的头部是 $s$ 的一个邻居 $u$ ,弹出 $u$ ,更新它所有的邻居的状态,把其中状态变化的入列。
3.弹出 $u$ 之后,在后面的计算中 $u$ 可能会被再次更新,此时 $u$ 需要重新入队,比如处理一个新的点 $v$ 的时候,它的邻居可能是之前处理过的 $u$ ,如果 $u$ 的状态变化了,把 $u$ 重新入队即可。
4.继续以上过程,直到队列为空,此时的状态就是起点 $s$ 到各点的最短距离。
下面是参考代码
void spfa(int s)
{
memset(dis, 0x3f3f3f3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
dis[s] = 0;
vis[s] = 1;
q.push(s);
while(!q.empty())
{
int x = q.front();
q.pop();
vis[x] = 0;
for(int i = head[x]; i; i = edge[i].next)
{
int y = edge[i].to, z = edge[i].w;
if(dis[y] > dis[x] + z)
{
dis[y] = dis[x] + z;
if(!vis[y])
{
vis[y] = 1;
q.push(y);
}
}
}
}
}判断负环
若图中存在一个环,并且环上的各边的边权之和为负,则称这个环为负环。含有负环的图不具有最短路,因为每一轮经过负环都会使 $dis$ 的值不断变小,我们用下图来进行举例:
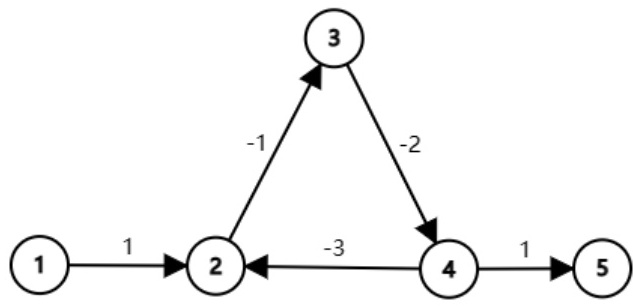
图中的点2,3,4之间形成了一个负环,当我们走进环里, $dis[2],dis[3],dis[4]$ 都会不断更新,导致我们无法走出负环。
接下来以P3385 【模板】负环](https://www.luogu.com.cn/problem/P3385))为例介绍两种判断负环的方法:
题目给定一个 $n$ 个点的有向图,要求出图中是否存在从顶点1出发能到达的负环。
Bellman-Ford
对于Bellman-Ford,判断负环的方法比较简单,如果是一个不具有负环的图,我们进行完 $n - 1$ 次松弛之后即可得到 $s$ 点到所有点的最短距离,并且接下来无论怎么松弛,都不会再有点被更新。可以利用这一点来判断图中是否有负环,先对所有边进行 $n - 1$ 次松弛,接着我们再对所有边进行一次松弛,此时如果有点被更新,则说明图中存在负环了。要注意使用上述方法求的是整个图中是否有负环存在,不能得到某一个点是否能到达负环,所以在本题中需要在松弛时多加一个条件dis[edge[j].u] != INF,以下是使用Bellman-Ford判断点 $s$ 是否能到达负环的参考代码:
void bellmanford(int s)
{
memset(dis, INF, sizeof(dis));
dis[s] = 0;
for (int i = 1; i <= n - 1; i++)
for (int j = 1; j <= tot; j++)
if (dis[edge[j].v] > dis[edge[j].u] + edge[j].w && dis[edge[j].u] != INF) // 求整张图中是否有负环则删去dis[edge[j].u] != INF这一条件
dis[edge[j].v] = dis[edge[j].u] + edge[j].w;
for (int i = 1; i <= tot; i++)
{
if (dis[edge[i].v] == INF || dis[edge[i].u] == INF)
continue;
if (dis[edge[i].v] > dis[edge[i].u] + edge[i].w)
{
printf("YES\n");
return;
}
}
printf("NO\n");
}SPFA
SPFA有两种方法来判断负环:
1.一个点入队的次数是否达到 $n$ 次
2.起点到某点的最短路径边数是否达到 $n$
这里我们主要介绍第二种方法的实现,用 $cnt[x]$ 表示从起点到点 $x$ 的最短路径包含的边数,每当 $dis[y] > dis[x] + w$ 更新 $dis[y]$ 时,也用 $cnt[y] = cnt[x] + 1$ 来更新 $cnt[y]$,此时若 $cnt[y] \geq n$ 则说明起点能到达负环。如果需要判断图中是否有负环,则需要建立一个超级源点,然后使用超级源点来跑SPFA算法。
void spfa(int s)
{
memset(dis, INF, sizeof(dis));
memset(vis, 0, sizeof(vis));
memset(cnt, 0, sizeof(cnt));
queue<int> q;
dis[s] = 0;
vis[s] = 1;
q.push(s);
while(!q.empty())
{
int x = q.front();
q.pop();
vis[x] = 0;
for(int i = head[x]; i; i = edge[i].next)
{
int y = edge[i].to, z = edge[i].w;
if(dis[y] > dis[x] + z)
{
dis[y] = dis[x] + z;
cnt[y] = cnt[x] + 1;
if(cnt[y] >= n)
{
printf("YES\n");
return;
}
if(!vis[y])
{
vis[y] = 1;
q.push(y);
}
}
}
}
printf("NO\n");
}差分约束
差分约束系统是一种特殊的 $n$ 元一次不等式,它包含 $n$ 个变量 $x_1, x_2, x_3, ···, x_n$ 和 $m$ 个约束条件,每个约束条件由两个变量做差构成,例如 $x_i - x_j \leq c_k$ ,我们需要求出一组解使所有的约束条件得到满足,否则判断为无解。
这个系统中的每个约束条件都可变形为 $x_i \leq x_j + c_k$ ,其中 $c_k$ 是常数,这与最短路算法中的三角形不等式 $dis[y] < dis[x] + z$ 非常相似,因此可以把每个变量 $x_i$ 当成图中的一个节点,每个约束条件视为一条边,例如 $x_i - x_j \leq c_k$ 就可以视为从节点 $j$ 向节点 $i$ 连接一条边权为 $c_k$ 的有向边。
接下来用P5960 【模板】差分约束算法](https://www.luogu.com.cn/problem/P5960))来举例
本题给出 $n$ 个未知数和 $m$ 个不等式,不等式形式如下,
$$ \begin{cases} x_{c_1}-x_{c_{1}^{'}}\leq y_1 \\ x_{c_2}-x_{c_{2}^{'}} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c_{m}^{'}}\leq y_m \end{cases} $$
求任意一组满足这个不等式的解。
上面的式子都可以化为 $x_{c_1} \leq y_1 + x_{c'_2}$
于是我们建立一张图,用给出的不等式来建边,在本题中就是从 $x_{c'm}$ 向 $x_{c_m}$ 建一条长度为 $y_m$ 的单向边,接着用SPFA来求解,如果图中出现负环,则说明无解,所以我们还需要建立一个超级源点来判断图中是否存在负环。最后,若不存在负环,输出超级源点到每个点的最短距离即可,若存在负环则无解。
但是大部分的题目中,不会将差分约束的约束条件设置的这么明显,这里再以[P3275 [SCOI2011]糖果](P3275 [SCOI2011]糖果 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))为例,讲一下其他类型的差分约束题目。(本题的hack数据会卡SPFA,需要进行缩点,但本专题的主题不是缩点,所以在这里只讲一下如何建图)
题目给出 $n$ 个小朋友和 $k$ 个要求,要求的类型有5种,如下所示,
- 如果 $X = 1$, 表示第 $A$ 个小朋友分到的糖果必须和第 $B$ 个小朋友分到的糖果一样多;
- 如果 $X = 2$, 表示第 $A$ 个小朋友分到的糖果必须少于第 $B$ 个小朋友分到的糖果;
- 如果 $X = 3$, 表示第 $A$ 个小朋友分到的糖果必须不少于第 $B$ 个小朋友分到的糖果;
- 如果 $X = 4$, 表示第 $A$ 个小朋友分到的糖果必须多于第 $B$ 个小朋友分到的糖果;
- 如果 $X = 5$, 表示第 $A$ 个小朋友分到的糖果必须不多于第 $B$ 个小朋友分到的糖果;
求出满足所有要求至少需要准备的糖果数,如果不能满足则输出-1。
由以上的要求可以得到下述不等式
$$ \begin{cases} X = 1 \quad x_A = x_B \\ X = 2\quad x_A < x_B \\ X = 3\quad x_A \geq x_B \\ X = 4\quad x_A > x_B \\ X = 5\quad x_A \leq x_B \end{cases} $$
将上式转化得
$$ \begin{cases} X = 1\quad x_A - x_B \leq 0, x_B - x_A \leq 0 \\ X = 2\quad x_A - x_B \leq -1 \\ X = 3\quad x_B - x_A \leq 0 \\ X = 4\quad x_B - x_A \leq -1 \\ X = 5\quad x_A - x_B \leq 0 \end{cases} $$
按上述要求建边即可,此时本题要求最小解,所以需要用SPFA跑最长路,将 $dis[y] > dis[x] + z$ 改为 $dis[y] < dis[x] + z$ 并在开始时将 $dis$ 重置为0即可。如果要求最大解,就正常跑最短路。
对于少数题目还会出现 $\frac{x_i}{x_j} \leq c_k$ 的情况,例如[P4926 [1007] 倍杀测量者](https://www.luogu.com.cn/problem/P4926),此时我们需要对两边同时取对数即可将乘法转化为加法,即 $\log_{2}{x_i} - \log_{2}{x_j} \leq \log_{2}{c_k}$ ,接着就可以利用差分约束求解了。
分层图
在一些题目中会对边的权值提供可选的情况,比如把某些边的边权变为0,分层图是解决这种问题的一种方法。
分层图的实现顾名思义,通过建立多个平行的图,再用某些特殊的点或边来将不同层的图连接起来,最后通过最短路算法来跑出最短距离,分层图的关键在于建图,而且在一些题上比较灵活。
下面用[P4568 [JLOI2011] 飞行路线](https://www.luogu.com.cn/problem/P4568)为例,讲一下分层图的建图。
题目大意是给出0到 $n - 1$ 一共 $n$ 个点,再给出 $m$ 条双向边,可以选择其中的 $k$ 条边并把它们的边权变为0,求出起点 $s$ 到终点 $t$ 的最短距离。因为每次将边的权值改为0对其他的边都没有影响,所以就可以将图复制成 $k + 1$ 层,接着将每条边的起点 $u_i$ 与下一层的该边的终点 $v_{i + 1}$ 建边,建好图之后跑Dijkstra即可,具体的建图代码如下
for(int i = 1; i <= m; i++)
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
add(u, v, w); //在第0层建边
add(v, u, w);
for(int j = 1; j <= k; j++)
{
add(u + j * n, v + j * n, c); //把边复制到第j层
add(v + j * n, u + j * n, c);
add(u + (j - 1) * n, v + j * n, 0); //连接上一层的起点与第j层的终点
add(v + (j - 1) * n, u + j * n, 0);
}
}如果转化为图的形式就是下面这样,图中的例子是有4个点且 $k = 2$ 的时候的情况
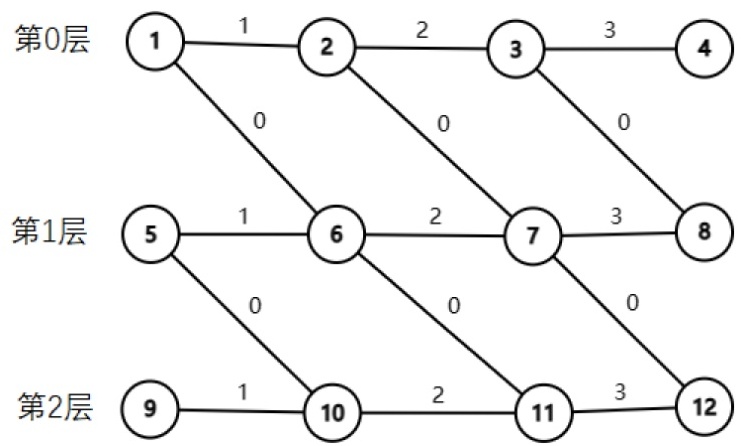
分层图的建图大致思路就和以上一样,但是在不同的题目上可能会有不同的变化,比如上面这道题就属于是有 $k$ 个操作可以改变边的权值;另一类题是有 $k$ 套边集,从一个边集的某点到另一个边集需要消耗一定代价,如NC26257 小雨坐地铁](https://ac.nowcoder.com/acm/problem/26257?&headNav=acm));还有一类题中的某些边权不确定,会随着起点入边的边权而变,需要用到一些动态规划的思想,如P1266 速度限制](https://www.luogu.com.cn/problem/P1266))。
题目列表
| 序号 | 题号 | 标题 | 题型 | 难度评级 |
|---|---|---|---|---|
| 1 | POJ - 1511 | Invitation Cards | Dijkstra | ⭐ |
| 2 | HDU - 4725 | The Shortest Path in Nya Graph | Dijkstra | ⭐⭐ |
| 3 | luogu P1119 | 灾后重建 | Floyd | ⭐⭐ |
| 4 | luogu P3385 | 【模板】负环 | Bellman-Ford/SPFA | ⭐ |
| 5 | POJ - 2240 | Arbitrage | Bellman-Ford/SPFA | ⭐⭐ |
| 6 | LightOJ - 1074 | Extended Traffic | Bellman-Ford/SPFA | ⭐⭐ |
| 7 | luogu P1993 | 小 K 的农场 | 差分约束 | ⭐ |
| 8 | SPOJ - INTERVAL | Intervals | 差分约束 | ⭐⭐ |
| 9 | luogu P2294 | [HNOI2005]狡猾的商人 | 差分约束 | ⭐⭐ |
| 10 | luogu P2474 | [SCOI2008]天平 | 差分约束 | ⭐⭐⭐ |
| 11 | luogu P4926 | [1007]倍杀测量者 | 差分约束 | ⭐⭐⭐ |
| 12 | luogu P4568 | [JLOI2011] 飞行路线 | 分层图 | ⭐ |
| 13 | NC26257 | 小雨坐地铁 | 分层图 | ⭐⭐ |
| 14 | luogu P3831 | [SHOI2012]回家的路 | 分层图 | ⭐⭐⭐ |
| 15 | luogu P1266 | 速度限制 | 分层图 | ⭐⭐⭐ |
参考资料
ACM图论-最短路 个人总结 - ice_dragon_grass - 博客园 (cnblogs.com)
学图论,你真的了解最短路吗? - 峰峰峰の妙妙屋 - 洛谷博客 (luogu.com.cn)
Bellman_Ford算法证明_bellman-ford算法证明_3Code_Love的博客-CSDN博客
差分约束学习笔记 - fty 的博客 - 洛谷博客 (luogu.com.cn)
《算法竞赛》 罗勇军、郭卫斌 清华大学出版社