并查集 - zhangfish's Blog

并查集的基本介绍

并查集是一种用于对元素进行分组并快速查找分组的数据结构，在ACM竞赛中十分常用，而且是接下来的最小生成树算法Krusal的前置知识。

并查集的基本原理是树，支持以下两种操作：

合并：合并两个元素所属集合（合并对应的树）
查询：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合

并查集的表示

通过一个数组 $f[N]$ 来表示并查集， $f[i]$ 就是 $i$ 所位于的集合，即 $i$ 所在的树上的根节点

并查集的操作

初始化

因为在进行操作前，每个元素所在的集合编号都应该是它自己，所以初始时需要对并查集初始化，操作如下:

void init(int n)
{
    for(int i = 1; i <= n; i++)
        f[i] = i;
}

查询

查询用于找到当前元素所在的树的根节点，也就是 $i$ 所在的集合

为了找到当前的根节点，我们需要不断向上移动：

查询.png

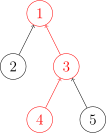
int find(int x) { return f[x] == x ? x : find(f[x]); }

但是如果我们的树在不断合并后变得很长时，这样查询的时间复杂度就会很高，所以我们在查询的时候可以对寻找父节点的路径进行压缩。简而言之就是找到集合的根节点后将节点从原来的地方直接接到根节点下，这样它的父节点就直接是根节点了，此时查询的时间复杂度为 $O(1)$

路径压缩.png

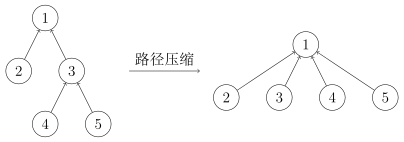
这是路径压缩的查询方法

int find(int x) { return f[x] == x ? x : f[x] = find(f[x]); }

合并

对两个集合进行合并就是将一个点的根节点连到另一个点的根节点上

合并.png

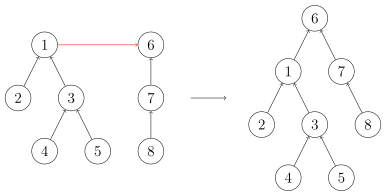
void merge(int x, int y)
{
    int fx = find(x), fy = find(y);                    //查询根节点
    if (fx != fy)                    //如果根节点不同
        f[fy] = fx;                    //将fy合并到fx上
}