一些图论基础算法,包括建图、图的遍历、最小生成树、拓扑排序
图的基本概念
图 是一个二元组 $G = \{V, E\}$ ,其中 $V = \{v_1, \dots, v_N\}$ 是点集,即包含了图中所有点的集合,点集中的点也被叫做 顶点 或 节点 ; $E = \{e_1, \dots, e_N\}$ 是边集,即图中包含了所有边的集合
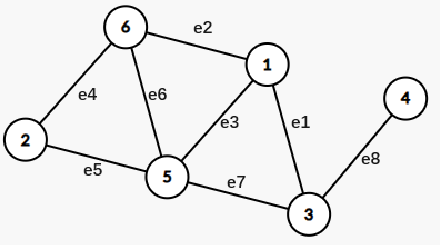
有向图 无向图
无向图 :图中的所有边都为 无向边 ,对于一个无向边 $e = (u, v)$ ,它的两个端点 $u, v$ 互相可达

有向图 :图中的所有边都为 有向边 ,对于一个有向边 $e = (u, v)$ ,它的起点是 $u$ ,终点是 $v$ ,且只能从 $u$ 到 $v$ ,无法从 $v$ 到 $u$
另外 有向边 也叫做 弧 ,边的终点被称为弧头,起始点被称为弧尾
度
度 :一个顶点的度就是与该顶点相关联的边的数目
出度 :有向图中,顶点所连接的 出边 的数量
入度 :有向图中,顶点所连接的 入边 的数量
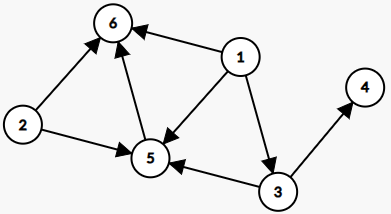
路径
路径(又称 简单路径):对于一个连接一连串顶点的边的序列,若其连接的点的序列中点两两不同,且连接的边也两两不同,则是一条路径
环(又称 简单回路/简单环 ):环是一条只有第一个和最后一个顶点重复的非空路径
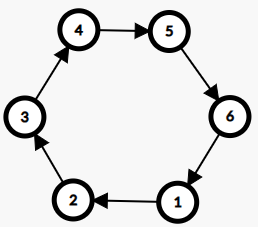
子图 :由图中部分节点以及这些节点间的边组成的图
连通
无向图
连通 :在无向图中,若从顶点 $u$ 到顶点 $v$ 有路径存在,则称 $u$ 和 $v$ 是连通的。
连通图 :若图中任意两个顶点都是连通的,那么就称这个无向图是连通图,否则是非连通图
连通分量 :极大连通子图
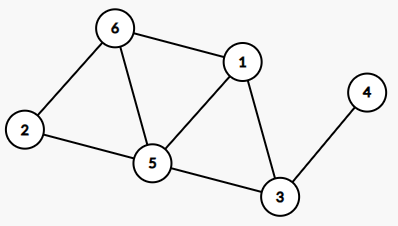
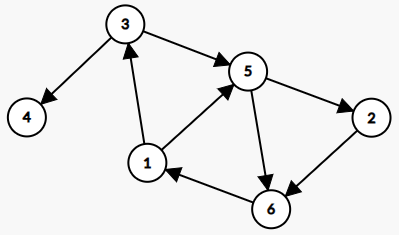
有向图
强连通 :在有向图中,若从顶点 $u$ 到顶点 $v$ 有路径存在,且从顶点 $v$ 到顶点 $u$ 也有路径存在,即 $u$ 和 $v$ 互相可达,则称 $u$ 和 $v$ 是连通的
强连通图 :在有向图中,若任意两个顶点都互相可达,则称该图为强连通图
强连通分量 :极大强连通子图
稀疏图/稠密图
若一张图的边数远小于其点数的平方,那么它是一张 稀疏图
若一张图的边数接近其点数的平方,那么它是一张 稠密图
图的存储
邻接矩阵
对于一个有 $n$ 个顶点的图 $G = (V, E)$ ,我们可以创建一个二位数组来记录任意两点间的相邻关系,这就是邻接矩阵
int edge[N][N];初始情况下,邻接矩阵中的值全为0,在有向图中,若 $u$ 有一条到 $v$ 的边,则修改 edge[u][v] = 1
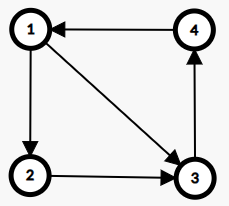
| 编号 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 |
| 4 | 1 | 0 | 0 | 0 |
无向图的邻接矩阵也是同理,只是要多加一条反向的边让这条边能双向可达,就是无向了,可以通过 edge[u][v] = 1, edge[v][u] = 1 实现
特点:
- 邻接矩阵只适用于没有重边(或重边可以忽略)的情况。
- 最显著的优点是可以 $O(1)$ 查询一条边是否存在。
- 在点数较多的图上效率很低,所以一般只会在稠密图上使用邻接矩阵。
邻接表
邻接表的思想是对图中每个顶点都开辟一个数组来存储与他相连的点,由于相邻的点会动态的增加,所以对于每个点,用 vector 来存储
在有向图中,若 $u$ 有一条到 $v$ 的边,则进行如下操作:
vector<int> edge[N]; //邻接表的创建,N为顶点的数目
edge[u].push_back(v); //u到v有一条边
//edge[v].push_back(u); //无向图则再添加一条反向边对于上面的图:
edge[1] = {2, 3};
edge[2] = {3};
edge[3] = {4};
edge[4] = {1};特点:
- 存各种图都很适合,除非有特殊需求(如需要快速查询一条边是否存在,且点数较少,可以使用邻接矩阵)
- 尤其适用于需要对一个点的所有出边进行排序的场合
链式前向星
本质上是以一个点为基础,后面跟一个链表,依次连着每一条以该点为起点的边
但这里我们不用指针来实现链表,而是采用结构体数组来模拟链表,先创建一个包含了终点,权值, $next$ 值的结构体数组 $edge[M]$ ,用于表示边,再用 $tot$ 作为数组下标,每加入一条边 $tot$ 就加1,在 $tot$ 处存入该边。
为了实现链表的结构,还需要加入链表元素的头节点,我们开辟一个数组 $head[N]$ , $head[i]$ 就表示第 $i$ 个顶点所连的边的编号。每当第 $i$ 个点加入新的边后,就将当前的编号接到要加入的边的编号后,再将加入的边的编号作为新的头节点编号。
如果用链表实现的话,上述的编号实际上就是链表中的节点,头节点编号就是头指针
链式前向星的创建:
struct Edge
{
int to, w, next; //to - 终点, w - 边权, next - 下一节点
}edge[M * 2]; //无向图的时候边数乘2
int head[N]; //头节点
int tot, n, m; //tot - 当前记录到第几条边, n - 点数, m - 边数
void addedge(int u, int v, int w) //u - 起点, v - 终点, w - 边权
{
edge[++tot].to = v;
edge[tot].w = w;
edge[tot].next = head[u]; //新加边的下一个点指向当前作为头的边
head[u] = tot; //将新加边作为头
}链式前向星的遍历:
for (int i = head[x]; i; i = edge[i].next)
{
...
}特点:
- 存各种图都很适合,但不能快速查询一条边是否存在,也不能方便地对一个点的出边进行排序。
- 优点是边是带编号的,有时会非常有用,而且如果
cnt的初始值为奇数,存双向边时i ^ 1即是i的反边 - 在一些对空间严格的题目上也可以使用,比邻接表vector写法的空间更好
拓扑排序
拓扑排序的概念
拓扑排序要解决的问题是给一个有向无环图的所有节点排序
有向无环图 (DAG) :没有环的有向图,DAG图是动态规划和记忆化搜索的结构基础
在一个 有向图 中,对所有的节点进行排序,要求没有一个节点指向它前面的节点。即当前仅当图是有向无环图时,拓扑排序有解,否则必有环
拓扑排序的步骤
- 从图中选择一个入度为零的点。
- 输出该顶点,从图中删除此顶点及其所有的出边。
- 不断重复以上步骤直到所有点被输出
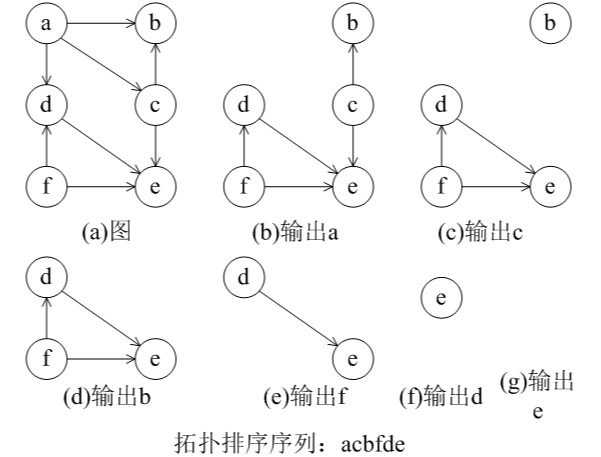
下面是拓扑排序的参考代码:
vector<int> edge[N]; // 邻接表建图
int ind[N]; // 入度
void topo(int n)
{
queue<int> q; // 用于存储顺序的队列
// priority_queue<int, vector<int>, greater<int>> q; 若拓扑排序需要按某种顺序可以用优先队列
vector<int> ans; // 拓扑排序结果
for (int i = 1; i <= n; i++) // 初始化队列, 将入度为0的元素放入队列
if (ind[i] == 0)
q.push(i);
while (!q.empty())
{
int cur = q.front();
// int cur = q.top(); 优先队列使用top()获取队首元素
q.pop();
ans.push_back(cur);
for (int i : edge[cur]) // 删除当前点, 将与当前点相邻的点的入度减1, 并更新队列
{
ind[i]--;
if (ind[i] == 0)
q.push(i);
}
}
}如果题目有顺序上的要求(如优先输出编号小的点),将上面代码中的队列改为优先队列即可。
从上面的代码可以看出,设顶点数为 $N$ ,边数为 $M$ ,则拓扑排序的时间复杂度为 $O(N + M)$
最小生成树
生成树与最小生成树的概念
含有连通图全部顶点并有n-1条边的连通子图,一个图的生成树可以有多种,最小生成树就是权值之和最小的生成树
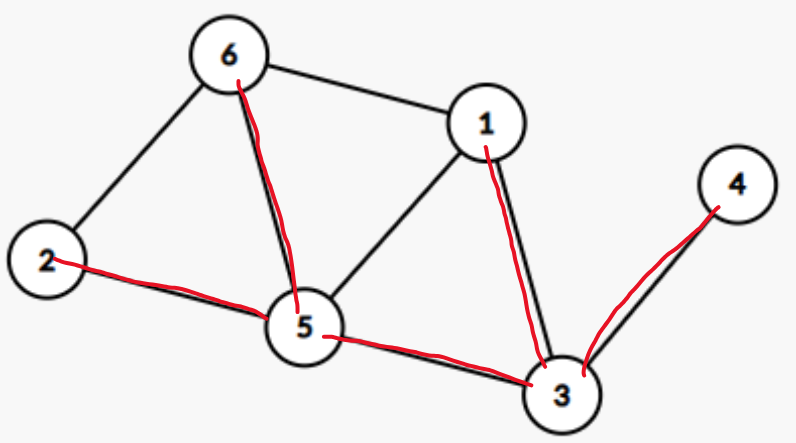
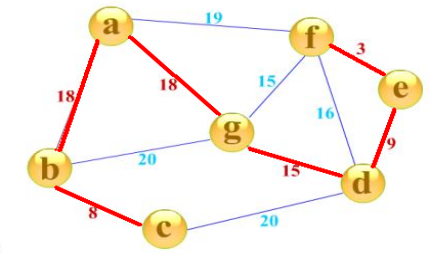
而对于一个有权图,每个边都具有边权,如果生成树中所有边的边权之和最小,则该生成树为最小生成树,下图就是一个最小生成树
Kruskal算法
Kruskal算法是一种常见并且好写的最小生成树算法,由 Kruskal 发明。该算法的基本思想是从小到大加入边,属于贪心算法
Kruskal算法的主要操作是 选边 ,先对所有的边进行从小到大的排序,接着按这个顺序遍历每一条边,从而优先选择较小的边,在选边的同时将与边相关的点放入已选的集合,若两点已经在同一集合里了,则跳过这条边,这一操作是为了防止选的边形成环。
设图中有 $M$ 条边则时间复杂度为 $O(MlogM)$
struct Edge
{
int u, v, w;
} edge[M];
int f[N];
int n, m; // n - 边数, m - 点数
bool cmp(Edge x, Edge y) // 结构体排序, 依据权值
{
return x.w < y.w;
}
int find(int x) // 并查集查询
{
if (x != f[x])
f[x] = find(f[x]);
return f[x];
}
void Kruskal()
{
for (int i = 1; i <= n; i++) // 初始化并查集
f[i] = i;
int sum = 0, cnt = 0; // sum - 最小生成树的权值和, cnt - 选择的边数
sort(edge + 1, edge + m + 1, cmp); // 从小到大对边排序
for (int i = 1; i <= m; i++)
{
int e1 = find(edge[i].u); // 检查边上的两点是否属于一个集合
int e2 = find(edge[i].v);
if (e1 != e2) // 两点不属于同一集合则选择这条边
{
f[e1] = e2; // 将两点放入同一集合中
sum += edge[i].w;
cnt++;
}
if (cnt == n - 1) // 选够了
break;
}
}题单
| 序号 | 题号 | 标题 | 题型 | 难度评级 |
|---|---|---|---|---|
| 1 | 洛谷 - P3916 | 图的遍历 | 图论基础 | ⭐ |
| 2 | HDU - 2094 | 产生冠军 | 图论基础 | ⭐ |
| 3 | 洛谷 - B3644 | 拓扑排序 / 家谱树 | 拓扑排序 | ⭐ |
| 4 | HDU - 1285 | 确定比赛名次 | 拓扑排序 | ⭐ |
| 5 | 洛谷 - P1113 | 杂务 | 拓扑排序 | ⭐⭐ |
| 6 | HDU - 4857 | 逃生 | 拓扑排序 | ⭐⭐ |
| 7 | 洛谷 - P1347 | 排序 | 拓扑排序 | ⭐⭐⭐ |
| 8 | 洛谷 - P3366 | 最小生成树 | 最小生成树 | ⭐ |
| 9 | 洛谷 - P2330 | 繁忙的都市 | 最小生成树 | ⭐ |
| 10 | 洛谷 - P1195 | 口袋的天空 | 最小生成树 | ⭐ |
| 11 | 洛谷 - P1194 | 买礼物 | 最小生成树 | ⭐⭐ |
| 12 | 洛谷 - P2820 | 局域网 | 最小生成树 | ⭐⭐ |
| 13 | 洛谷 - P4047 | 部落划分 | 最小生成树 | ⭐⭐⭐ |
| 14 | AtCoder - abc328_e | Modulo MST | 最小生成树 | ⭐⭐⭐ |
| 15 | 洛谷 - P2632 | Explorer | 最小生成树 | ⭐⭐⭐⭐ |